
In 1994 Melinda Green, Don Hatch, and Jay Berkenilt created the so-called "MagicCube4D", which is a 4-dimensional analogue of the Rubik's Cube in Java consisting of hypercubes from 2x2x2x2 to 5x5x5x5. With many more possible states this object is much more difficult to solve. So far only 78 people have managed to solve it. The geometric shape of this cube is a tesseract, which has each line divided into 3 equal parts for the standard puzzle, the result of this is that in addition to the 1, 2, and 3 colored pieces of the 3-dimensional cube there is a fourth type of piece with 4 colors each, which are at the vertices.
Como resolver el Cubo de Rubik en 22 jugadas.
In 2006 Roice Nelson and Charlie Nevill created the 5-dimensional "Magic Cube 5D" model from 2x2x2x2x2 to 5x5x5x5x5 which so far has been solved by only twelve people. In this puzzle there are also pieces with five colors which are also on the vertices.
Número de posibles combinaciones-
El cubo de Rubik es un famoso juego tipo Puzzle que fue inventado en el año 1974 por Erno Rubik, de Hungría. Desde ese momento el juego se popularizó y llegó a ser conocido en todos los rincones del mundo.
Debido a que es un juego de cierta dificultad y que requiere de gran destreza y capacidad mental, todos empezaron a jugarlo, y el cubo empezó a ser objeto de análisis de los científicos.
En 1981, el matemático Morwen Thistlethwaite, de la universidad de Tenesse en los Estados Unidos, logró demostrar al mundo que este juego podía ser siempre resuelto en menos de 52 movimientos, no importaba cual fuera el orden en el que se encontrara el cubo.
En 1992 el holandés Hans Kloosterman logró reducir este límite, demostrando que cualquier situación en el cubo de Rubik podría ser resuelta en menos de 42 movimientos. Pero en 2008 de nuevo los estadounidenses redujeron este récord, y lograron mostrar que el Cubo de Rubik podría ser resuelto en 22 jugadas. En el año 2010, un grupo de científicos de todo el mundo, demostraron que eran aún menos: Siempre se puede resolver el puzzle con 20 jugadas o menos.

El cubo puede tener 43.252.003.274.489.856.000 formas de orden diferentes, combinaciones distintas. Esto demuestra la dificultad para realizar estos cálculos y llegar a cifras exactas. Sin embargo, las matemáticas modernas y la tecnología han permitido llegar a este punto de análisis. Y tú, ¿todavía esperas que alguien te diga cómo resolver el cubo de Rubik?
Número de combinaciones posibles.

Podemos combinar entre sí de cualquier forma todos los vértices del cubo, lo que da lugar a 8!,! posibilidades. Con las aristas pasa lo mismo; es decir, que podemos combinarlas como se desee, lo que da lugar a 12!,! posibilidades, pero la permutación total de vértices y aristas debe de ser en total par, lo que nos elimina la mitad de las posibilidades. Por otra parte, podemos rotar todos los vértices como queramos salvo uno sin cambiar nada más en el cubo. La orientación del último vértice vendrá determinada por la que tengan los otros siete, y esto nos crea 3^7,! posibilidades. Igual debe ocurrir con las aristas, pues aparecen 2^{11},! posibilidades más. En total tendremos que el número de permutaciones posibles en el Cubo de Rubik es de:
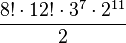
= 43.252.003.274.489.856.000
Es decir, cuarenta y tres trillones doscientos cincuenta y dos mil tres billones doscientos setenta y cuatro mil cuatrocientos ochenta y nueve millones ochocientas cincuenta y seis mil permutaciones.
Existen muchas variaciones del Cubo de Rubik original y también de rompecabezas parecidos, de forma cúbica o de otras distintas. Entre las variaciones cúbicas destaca el "Cubo Mágico" el cual es mecánicamente idéntico al original, pero usa números de colores en sus caras de tal manera que la única forma de resolverlo es que todos los números estén al derecho en la misma cara, adicionalmente los números de las caras forman cuadrados mágicos los cuales pueden tener todos la misma constante. Un cubo muy similar es el cuboku en el cual el objetivo es formar sudokus con los números de las caras. O un cubo cortado de manera no paralela a las caras: el Skewb.
Otras incluyen colocar imágenes en lugar de colores o diseños de colores que confundan al que resuelve, como colocar en un 4x4x4 cuatro colores distintos en cada cara para un total de 24 colores distintos. O también reducir el número de colores a 3.
Entre las formas no cúbicas destacan los cubos extendidos que tienen una o más capas adicionales, las cuales pueden ser completa o parcialmente funcionales. También están los rompecabezas basados en mapamundis y otros sólidos platónicos: el Skewb diamante, el Megaminx, el Pyraminx o el Dogic entre otros. Para la mayoría de estas variaciones es posible pensar en otros rompecabezas que estén partidos en un mayor número de piezas de la misma manera que La Venganza de Rubik por ejemplo, así como distintas maneras de colorearlos.
Pyraminx resuelto.

Durante el auge del cubo, la empresa de videojuegos Atari lanzó sus cartuchos para consola Atari 2600 llamados "Rubik's Cube" (CX2698), "Atari Video Cube" (reedición que cambió el nombre por razones de copyright, CX2670) y el prototipo "Rubik's Cube 3D" que no salió al mercado.
Variaciones extra dimensionales.

En 1994 Melinda Green, Don Hatch, y Jay Berkenilt crearon el llamado "MagicCube4D", el cual es un modelo tetradimensional análogo de el Cubo de Rubik en Java el cual consiste en hipercubos desde 2x2x2x2 hasta 5x5x5x5. Con muchos más estados posibles este objeto es mucho más difícil de resolver. Hasta ahora sólo 78 personas lo han conseguido resolver. La forma geométrica de este cubo es de un teseracto, el cual tiene cada línea dividida en 3 partes iguales para el rompecabezas estándar, el resultado de esto es que además de las piezas de 1, 2, y 3 colores del cubo de 3 dimensiones existe un cuarto tipo de pieza con 4 colores cada una, las cuales están en los vértices.
En 2006 Roice Nelson y Charlie Nevill crearon el modelo pentadimensional "Magic Cube 5D" desde 2x2x2x2x2 hasta 5x5x5x5x5 que hasta ahora ha sido resuelto sólo por doce personas. En este rompecabezas existen además piezas con cinco colores las cuales están también sobre los vértices.
Fuente imágenes: Rubik.










0 commentarios:
No insertar mensajes clicables en los comentarios, caso contrario el mismo será eliminado.
Si te hemos ayudado con el artículo o con las respuestas a los comentarios puedes compartirlos en Twitter, Facebook, Flipboard, Linkedin, Mastodon, Pinterest, Scoop,it, Bluesky, Threads o Tumblr.